Textures can be created and defined as two-dimensional images which are mapped onto a surface. Textures of a surface can be set in two different ways. A texture can be set as a viewing attribute so that all instances of a surface have the same texture (see Appendix II), or it can be set during string interpretation so that instances of a surface may have different textures. Textures can be set during string interpretation by the following module:
6.1 Textured Bicubic Surfaces
To map the texture onto the surface, there are two ways of transforming the object coordinates (x,y,z) into the texel (pixel of the texture image) coordinates (u,v)[6]:
 |
|---|
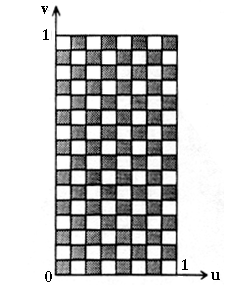| Figure 6.1 u,v coordinate system |
 |
 |
|---|---|
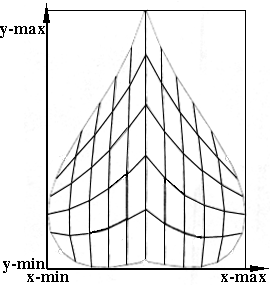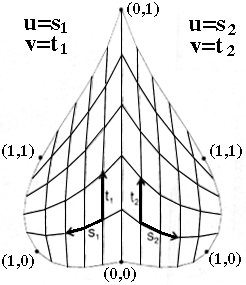
| Figure 6.2 Map onto each patch |
Figure 6.3 Map onto entire surface u=(x-(x-min))/((x-max)-(x-min)) v=(y-(y-min))/((y-max)-(y-min)) |
|
Example:
The following L-System maps a texture onto a bicubic surface
#define INDEX 1 #define LSTEPS 200 #define Lr 0.01 #define LFN(t,L,D)(3*(L)/(D)^2*(t)^2-2*(L)/(D)^3*(t)^3) #define LR 2 #define WR 2 #define SR 2 #define PAR 2 #define RAR 2.67 #define TAR 2 #define RIBPIT1_1 200 #define RIBPIT2_1 233 #define RA1_1 RIBPIT1_1-180 #define RA2_1 RIBPIT2_1-180 #define RIBLEN0_1 2 #define RIBLEN1_1 2 #define RIBLEN2_1 3 #define CROSS0_1 0.1 #define CROSS1_1 1.2 #define CROSS2_1 1.8 #define CROSS3_1 1.1 #define SEG00_1 0.1 #define SEG01_1 1.3 #define SEG10_1 1.6 #define SEG11_1 1.7 #define CROSSPIT0_1 132 #define CROSSPIT1_1 256 #define CROSSPIT2_1 259 #define CROSSPIT3_1 228 #define SEGPIT0_1 200 #define SEGPIT1_1 180 #define CP0_1 CROSSPIT0_1-180 #define CP1_1 CROSSPIT1_1-180 #define CP2_1 CROSSPIT2_1-180 #define CP3_1 CROSSPIT3_1-180 #define SP0_1 SEGPIT0_1-180 #define SP1_1 SEGPIT1_1-180 #define CROSSTRN0_1 180 #define CROSSTRN1_1 180 #define CROSSTRN2_1 180 #define CROSSTRN3_1 143 #define SEGTRN0_1 98 #define SEGTRN1_1 107 #define CT0_1 CROSSTRN0_1-180 #define CT1_1 CROSSTRN1_1-180 #define CT2_1 CROSSTRN2_1-180 #define CT3_1 CROSSTRN3_1-180 #define ST0_1 SEGTRN0_1-180 #define ST1_1 SEGTRN1_1-180 lsystem: 1 derivation length: LSTEPS axiom: L L --> @Tx(INDEX)UVWXYZ U --> @PS(0)[+(0,0,90,90+CT0_1,0,TAR)&(0,0,0,CP0_1,0,PAR) f(0,0,0,CROSS0_1,0,WR)@PC(0,0,0)[+(0,0,0-45,ST0_1,0,TAR) &(0,0,0,SP0_1,0,PAR)f(0,0,0,SEG01_1,0,SR)@PC(0,1,0)] -(0,0,0-135,180-ST0_1,0,TAR)^(0,0,0,SP0_1,0,PAR) f(0,0,0,SEG00_1,0,SR)@PC(0,0,1)] V --> [-(0,0,90,90+CT0_1,0,TAR)&(0,0,0,CP0_1,0,PAR)f(0,0,0,CROSS0_1,0,WR) @PC(0,0,3)[-(0,0,0-45,ST0_1,0,TAR)&(0,0,0,SP0_1,0,PAR) f(0,0,0,SEG01_1,0,SR)@PC(0,1,3)]+(0,0,0-135,180-ST0_1,0,TAR) ^(0,0,0,SP0_1,0,PAR)f(0,0,0,SEG00_1,0,SR)@PC(0,0,2)] W --> f(0,0,0,RIBLEN0_1,0,LR)[+(0,0,90,90+CT1_1,0,TAR)&(0,0,0,CP1_1,0,PAR) f(0,0,0,CROSS1_1,0,WR)@PC(0,1,1)][-(0,0,90,90+CT1_1,0,TAR) &(0,0,0,CP1_1,0,PAR)f(0,0,0,CROSS1_1,0,WR)@PC(0,1,2)] X --> &(0,0,0,RA1_1,0,RAR)f(0,0,0,RIBLEN1_1,0,LR)[+(0,0,90,90+CT2_1,0,TAR) &(0,0,0,CP2_1,0,PAR)f(0,0,0,CROSS2_1,0,WR)@PC(0,2,1)] [-(0,0,90,90+CT2_1,0,TAR)&(0,0,0,CP2_1,0,PAR)f(0,0,0,CROSS2_1,0,WR) @PC(0,2,2)]&(0,0,0,RA2_1,0,RAR)f(0,0,0,RIBLEN2_1,0,LR) Y --> [+(0,0,90,90+CT3_1,0,TAR)&(0,0,0,CP3_1,0,PAR)f(0,0,0,CROSS3_1,0,WR) @PC(0,3,0)[+(0,0,0-135,ST1_1,0,TAR)&(0,0,0,SP1_1,0,PAR) f(0,0,0,SEG11_1,0,SR)@PC(0,3,1)]-(0,0,0-45,180-ST1_1,0,TAR) ^(0,0,0,SP1_1,0,PAR)f(0,0,0,SEG10_1,0,SR)@PC(0,2,0)] Z --> [-(0,0,90,90+CT3_1,0,TAR)&(0,0,0,CP3_1,0,PAR)f(0,0,0,CROSS3_1,0,WR) @PC(0,3,3)[-(0,0,0-135,ST1_1,0,TAR)&(0,0,0,SP1_1,0,PAR) f(0,0,0,SEG11_1,0,SR)@PC(0,3,2)]+(0,0,0-45,180-ST1_1,0,TAR) ^(0,0,0,SP1_1,0,PAR)f(0,0,0,SEG10_1,0,SR)@PC(0,2,3)];(127)@PD(0,8,8) endlsystem
|
6.2 Textured Generalized Cylinders
Textures on generalized cylinders can only be set during string interpretation by the module @Tx(index). The texel coordinate system is specified in the following way: the u coordinate goes around the segment circumference, where u is an element of [0,1], and the v coordinate increases along the cylindrical axis in such a way that the aspect ratio of the image pixels mapped onto the surface is always 1. The v coordinate can be computed using the following equation:
where l is the segment length, c is the circumference of the base disk, Rx and Ry are sizes of the texture image, and v0 is the final texel coordinate from the previous line segment (see Figure 6.4)[7].
v0=0 is the value of the very first line segment. The starting value for the subsequent segment is the last value of texel v.
The image is repeated along the stem and the left and right sides of the texture are aligned.
 |
|---|
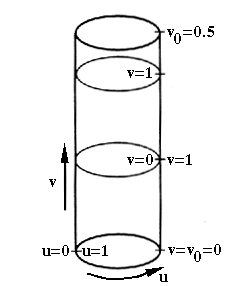u,v coordinate system |
|
Example:
The following L-System maps a texture onto a generalized cylinder.
#define STEPS 1 #define CLEN 0.35 #define NR 5 #define LEN 1 #define LENLOW 1 #define LENMID 1 #define LENUP 1 #define RIGHT 45 #define LEFT 45 Lsystem: 1 derivation length: STEPS Axiom: \(0),(95)#(2)@Tx(1)@Gs F(LENLOW*2) +(LEFT) F(LENMID*2) -(RIGHT) F(LEN*3) F(LENUP*2)@Ge(NR) homomorphism F(x) --> f(x)@Gc(NR) endlsystem
|
6.3 Textured Polygons
Textures on polygons can only be set during string interpretation by
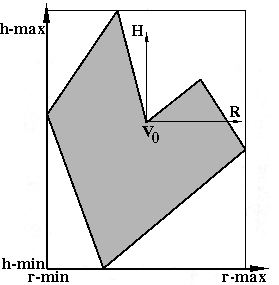
the module @Tx(index). Polygon vertices h and
r are used to determine texture coordinates u and
v. The turtle's heading vector of the first polygon vertex
v0 is used to define the h axis
and the turtle's right vector (left vector in opposite direction)
of the first polygon vertex v0 is used to define the r axis. The h and r coordinates are scaled to the interval [0,1] to obtain the u and v texture coordinates (see Figure 6.5)[8].
 |
|---|
| Figure 6.5 Map onto entire surface u=(r-(r-min))/((r-max)-(r-min)) v=(h-(h-min))/((h-max)-(h-min)) |
|
Example:
The following example maps a texture onto a polygon.
#define STEPS 1
#define INDEX 1
Lsystem: 0
derivation length: STEPS
Axiom: @Tx(INDEX){.-(45)F(4).+(90)F(4).+(90)F(4).+(90)F(4).}
endlsystem
|
 |
 |
 |
 |
 |
Preface Parameters Appendix I Appendix II References |
|---|---|---|---|---|---|
| Index | Circles and Spheres | Generalized Cylinders | Surfaces | Textures |
